In the past two weeks, I went through more tutorials and learned how to select, sort, and rank columns in a matrix or a data frame. However, I am more thrilled to talk about the “if-else” logic expression as I noticed something strange while trying out myself. If you are interested in studying this topic yourself, you may find this edx video tutorial and this website to be helpful. They are both free.
The first thing I entered was:
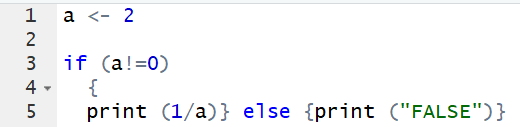
This is the simplest “if-else” expression. The first line means set “a” as a variable and a = 2. The third to the fifth line is the logic expression. If “a” doesn’t equal to 0 (in R, “!=” means “≠”), the output would be 1/a. Otherwise (if a = 0), the output should be “FALSE”. This is what happens when we run these lines.
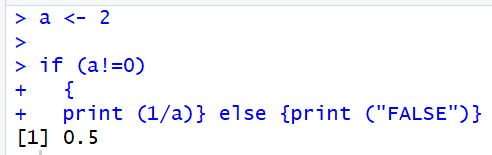
Obviously, the logic works. We have a = 2, so a ≠ 0. This matches with the condition that the result = 1/a = 1/2 = 0.5. However, if we start “else” in a new line, then something strange will happen.

When we start “else” in a new line, the R Studio says there is an error. If we run the codes, R Console would show the following:

This triggers my curiosity, since this is the only time that starting a new line would lead to different results. Let me explain it quickly using another example.

In R, the two sections in Code 3 mean exactly the same thing. The only difference is the first section occupies 1 line while the second section occupies 4. They both mean read the document “oasis_cross-sectional.csv” as a data frame and name the data frame as “A”. This example is not an exception. In fact, starting codes from a new line work in most expressions I learned. However, it doesn’t work in the “if-else” expression. To figure out the answer, I did some research on the curly bracket “{” and “}” in R.
According to “R in a Nutshell, 2nd Edition” by Joseph Adler, curly brackets (braces) are “used to evaluate a series of expression” or “used to group a set of operations in the body of a function” (Adler). This hints that the curly brackets only work when there is another corresponding expression, like “if-else. ” If there is no such expressions, curly brackets would have no effects.
Why this matters? Obviously, curly brackets only work when you have pairs of heads and tails. The computer only reads the statement in between. Here is an example:

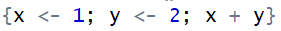
If you compare Code 4 and Code 5, you would notice Code 4 is missing the tail curly bracket ( } ). So, your computer would read Code 4 as a bunch of characters and Code 5 as a statement.
Again, curly brackets need to work with another expression. My hypothesis is the head bracket would find the first expression in front of itself and match with it. Then, the corresponding tail bracket will close the statement. This explains why Code 1 works when we have started the head bracket in a new line. The bracket would automatically find the “if” expression and match with it.
However, the “else” expression doesn’t do the same work. When you start “else” in a new line, it wouldn’t find the corresponding “if.” I believe this is not a flaw, but an intentional design. A head bracket always needs another expression, but “else” doesn’t always need “if”, it may match with other expressions, like “else if”. So letting “else” find its own expression would lead to many logic errors.
To test my conclusion, I used the following codes:
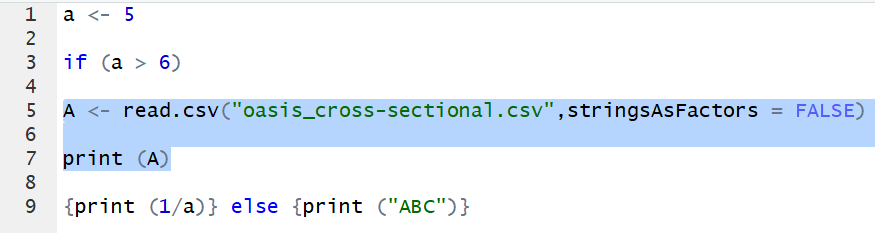
In Code 6, the highlighted lines are the ones I inserted intentionally for testing. According to our hypothesis, the first head curly bracket in line 9 would find the statement in front of it. This means line 7 would match with line 9. At the same time, the “if” expression in line 3 would match with line 5, as after we give the condition (a > 6), it automatically considers line 5 as the “so what.” This is what happens when we run the codes:

Only the first line works! The logic function “if-else” fails as the brackets can no longer find the correct expression. In comparison to Code 2 and Output 2, even though R identify both errors as “unexpected ‘else’,” it is obvious that the problem with Code 2 is the tail bracket while the problem with Code 6 is the head bracket. In addition, line 7 fails to work as line 5. Line 5, the line that is supposed to match with line 7, is now matched with line 3 (as shown by the “+” sign in the output). This means we no longer have a definition for A, so we can’t find it.
This is the end of my main topic. In this blog, we successfully found a problem and established some reasonable conclusions. Of course, these conclusions may be wrong, but the process of identifying and solving a problem was fun for me! When codes fail to run, I believe it is always important to read the error notice to identify the issue. Furthermore, it is also helpful to reflect on and identify the deeper reason that leads to the error.
Works Cited
Adler, Joseph. R in a Nutshell. 2nd ed., Sebastopol, O’Reilly Media, 2012. O’REILLY, http://www.oreilly.com/library/view/r-in-a/9781449358204. Accessed 29 Apr. 2019.
“ifelse.” RDocumentation, www.rdocumentation.org/packages/base/versions/3.5.3/topics/ifelse. Accessed 29 Apr. 2019.
Irizarry, Rafael. “Basic Conditionals.” Edx.org. Lecture.